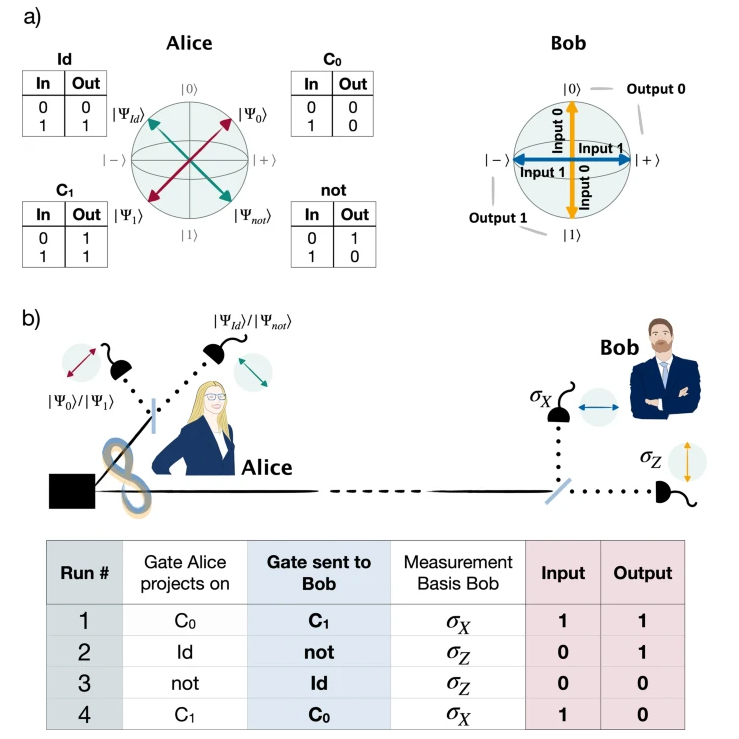
Quantum technology allows for unparalleled levels of data and software protection. Probabilistic one-time programs harness these capabilities for quantum-assisted classical computations by encoding classical software in small quantum states resulting in computer programs that can be used only once.
Such self-destructing one-time programs facilitate a variety of applications reaching from software distribution to one-time delegation of signature authority. Whereas previous experiments demonstrated the feasibility of such schemes, the practical applications were limited. Here we present an improved protocol for one-time programs that resolves major drawbacks of previous schemes, by employing entangled qubit pairs. This results in four orders of magnitude higher count rates and the ability to execute a program long after the quantum information exchange has taken place. We implement a one-time delegation of signature authority over an underground fiber link between university buildings in downtown Vienna, emphasizing the compatibility of our scheme with prepare-and-measure quantum internet networks.
Introduction
Computational algorithms touch almost every aspect of modern life. In light of continuous data breaches and increasingly stricter legislation on data protection, it would be desirable to reduce the amount of private user data leaked in a computation without forcing software owners to completely reveal their source code. Quantum computers have been shown to offer significant advantages in this area. A prominent example is blind quantum computation, where an almost classical client can delegate a quantum computation such that the quantum server cannot learn any information regarding the input, output and algorithm of the quantum computation. 1,2,3,4,5 While protocols such as this clearly demonstrate that quantum systems can provide powerful enhancements to the privacy of computations, full scale quantum computers still present significant technical challenges. Thus, it is of particular interest to investigate hybrid quantum-classical solutions which might allow for quantum enhancements of classical technology as well.
A promising direction of investigation is to use small quantum systems (such as single photons, which can be readily generated and manipulated by state-of-the-art quantum technology) to augment classical computers, and in particular to use them as a resource to increase the privacy of computations. A well-known example of such hybrid systems are quantum key distribution protocols.6,7 Recently, another such hybrid system was demonstrated for probabilistic one-time programs.8 One-time programs are a cryptographic primitive for performing secure computation in which a server provides a client with a software in such a way that the client can obtain only one input-output pair (x, f(x)) before the program is destroyed. Both the input of the client and the software of the server remain private (up to the information that is leaked by the input-output pair). One-time programs are considered as a powerful building block for many cryptographic tasks and could be used for applications such as software licensing, one-time delegation of signing abilities and electronic voting schemes. It has, however, been shown that perfect information theoretically secure quantum and classical one-time programs are impossible to implement without the use of one-time self-destructing hardware (hardware which is automatically destroyed after a single use).9,10,11 These no-go results can be circumvented by allowing for the possibility of error in the program outcome resulting in probabilistic one-time programs.8
References:
- Broadbent, A., Fitzsimons, J. & Kashefi, E. Universal blind quantum computation. In Proceedings of 50th Annual IEEE Symposium on Foundations of Computer Science, FOCS’09. 517–526 (2009).
- Dunjko, V., Fitzsimons, J. F., Portmann, C. & Renner, R. Composable security of delegated quantum computation. Adv. Cryptol.—ASIACRYPT 2014 8874, 406–425 (2014).
- Morimae, T. & Fujii, K. Blind quantum computation protocol in which alice only makes measurements. Phys. Rev. A 87, 050301 (2013).
- Barz, S. et al. Demonstration of blind quantum computing. Science 335, 303–308 (2012).
- Greganti, C., Roehsner, M.-C., Barz, S., Morimae, T. & Walther, P. Demonstration of measurement-only blind quantum computing. New J. Phys. 18, 013020 (2016).
- Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In Proceedings of IEEE International Conference on Computers, Systems and signal processing, vol. 175 (1984).
- Ekert, A. K. Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
- Roehsner, M.-C., Kettlewell, J. A., Batalhão, T. B., Fitzsimons, J. F. & Walther, P. Quantum advantage for probabilistic onetime programs. Nat. Commun. 9, 1–8 (2018).
- Broadbent, A., Gutoski, G. & Stebila, D. Quantum one-time programs. In Proceedings of Advances in Cryptology—CRYPTO 2013. Part II 344–360 (2013).
- Goldwasser, S., Kalai, Y. T. & Rothblum, G. N. One-time programs. In Proceedings of Advances in Cryptology—CRYPTO 2008. 39–56 (2008).
- Liu, Y.-K. Single-shot security for one-time memories in the isolated qubits model. In Proceedings of Advances in Cryptology—CRYPTO 2014. 19–36 (2014).
- PUBLICATION
Marie-Christine Röhsner, Joshua A. Kettlewell, Joseph Fitzsimons, Philip Walther;
Probabilistic one-time programs using quantum entanglement,
npj Quantum Information 7/98 (2021); DOI: 10.1038/s41534-021-00435-w
Probabilistic one-time programs using quantum entanglement,
npj Quantum Information 7/98 (2021); DOI: 10.1038/s41534-021-00435-w